Rumus Perhitungan Mesin Bubut

Proses bubut atau turning masih banyak digunakan didalam industri dewasa ini, begitu juga di Indonesia, berikut adalah rumus-rumus penting yang digunakan untuk menghitung berbagai parameter permesinan dari mesin bubut
Definisi

n  : putaran spindle (rpm)
fn : pemakanan (mm)
ap: kedalaman pemotongan (mm)
perlu diperhatikan arah dari proses pengerjaan bila memulai perhitungan, kenali dahulu proses apa yang terjadi apakah facing, atau proses pemakanan ke arah spindle ataukah pembuatan groove.
bila perhitungan untuk groove maka lebar dari pahat/cutting tool adalah kedalaman pemotongan. sedangkan proses perhitungan untuk taper dapat didekati dengan metode trapesium, metode yang lebih baik tentunya dengan menghitung setiap pergerakan cutting tool.

Kecepatan Pemotongan
dihitung dari putaran per menit terhadap diameter benda kerjanya, sering juga disebut dengan kecepatan pada permukaan

n = putaran benda kerja (rpm)
D = Diameter benda kerja (mm)
Vc = kecepatan pemotongan (m/menit)
Kecepatan Putaran Benda Kerja (RPM)
dihitung dari jumlah putaran setiap menitnya, konstanta 1000 adalah perubahan dari mm ke meter

Metal removal rate
dihutng dari kecepatan pemotongan, dikalikan dengan kedalaman pemotongan dan pemakanannya,Vc = Kecepatan pemotongan (m/menit), sedangkan simbol lainya sama artinya dengan sebelumnya.

 Kebutuhan Daya (Net Power)
perhitungan daya yang dibutuhkan (Pc) dalam kilowatt sebenarnya dapat dicari secara analitis maupun secara empiris, umumnya didapatkan dengan mengasumsikan besarnya daya adalah 80 % dari daya motor, sedangkan proses perhitungan didapatkan dari

dengan kc adalah gaya potong spesifik, Kc dihitung dengan

dengan Y0 adalah sudut chip, dan hm adalah ketebalan chip(mm) perhatikan gambar berikut, bila menggunakan insert untuk pemotongan bubut, maka pemilihan parameter sedikit berbeda, meskipun secara pengertian sama persis apa yang harus dihitung

Lama Waktu Pemotongan

dengan lm adalah panjang benda kerja yang dipotong, untuk benda berbentuk lurus tentunya mudah bukan, namun untuk benda berbentuk tirus, panjang benda kerja dihitung dengan

Dm1 = diameter terbesar, Dm2=diameter terkecil, semua satuan dalam mm

Rumus Menghitung Panjang Jurai Untuk Menghitung Luasan Atap

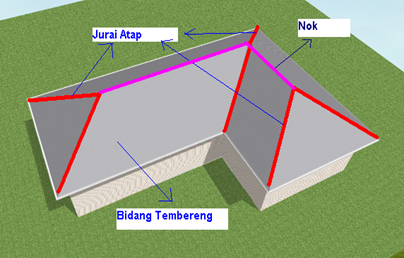
Sebelum menghitung kebutuhan atap, maka harus dihitung dahulu luasan atapnya (dalam hal ini adalah : luasan bidang tembereng). Luasan tembereng bisa dihitung jika panjang jurai atapnya sudah diketahui.

Untuk menghitung panjang jurai bisa digunakan rumus berikut :

Mungkin teman2 pasti bertanya-tanya, darimanakah asal dari rumus tersebut?

Jawabannya :

sederhana kok, hanya kolerasi hitungan matematika saja, yaitu penggabungan antara konsep phytagoras dan rumus sudut

Perhatikan gambar dibawah ini :

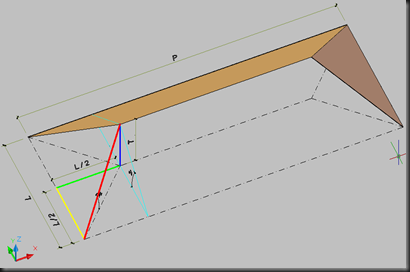
(Gb.1)

Garis yang berwarna merah = Jurai Atap, Garis yang berwarna kuning = garis bantu horizontal, Garis yang berwarna hijau = garis bantu vertikal, Garis yang berwarna biru = tinggi kuda2 (tinggi dari alas ke nok)

 

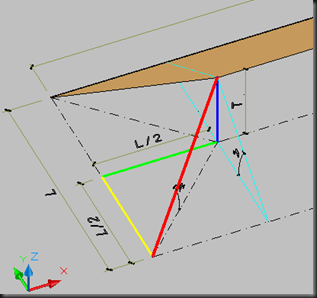
(Gb.2)

Konsepnya :

Jika panjang dari garis biru di kuadratkan, panjang dari garis hijau di kuadratkan, dan panjang dari garis kuning di kuadratkan, kemudian hasilnya dijumlahkan, dan setelah itu hasil dari penjumlahan tersebut diakarkan, maka akan didapat panjang dari garis merah

- Atau secara redaksionalnya adalah :

Akar dari jumlah garis biru kudarat ditambah garis hijau kuadrat, ditambah garis kuning kuadrat itu sama dengan panjang dari garis merah (garis jurai)

- Jadi kalau konsep diatas dijadikan sebuah perumusan maka bisa ditulis :

Panjang dari jurai (garis warna merah) :……….(rumus.1)

Nb : Ndak percaya?!…Silahkan anda buktikan sendiri!

Baik!, sekarang kita kembali ke perumusan diatas, lihat Gb.2

Nah…katakanlah atapnya memiliki lebar sepanjang L (lihat gbr diatas), maka akan didapat panjang dari garis hijau dan kuning sebagai berikut :

1. garis hijau     = L/2
2. garis kuning  = L/2

Trus, bagaimana untuk panjang dari garis biru ?

Untuk menghitung garis biru, bisa dijabarkan sebagai berikut (lihat yang saya lingkari pakai warna merah)

Panjang dari garis tersebut adalah :

tan α = ( panjang dari garis tersebut / setengah panjang L )

panjang dari garis tersebut = tan α x setengah panjang L

                                    = tan α  x  (0.5 x L)

Jadi panjang garis biru    = tan α  x 0.5 L

Nah…jika nilai2 tersebut yaitu :

1. Panjang garis hijau     = L/2
2. Panjang garis kuning  = L/2
3. Panjang garis biru  = tan α  x 0.5 L

disubstitusi pada  rumus.1  diatas, maka akan didapatkan harga/rumus sbb :

Cukup mudah kan…..Baik sekarang kita menginjak ke contoh kasus

Contoh diambil pada posting sebelumnya

Sebuah rumah dengan model atap Hip Roof (atap perisai) dengan ukuran atap sedemikian rupa, dan rencananya akan memakai penutup atap genteng beton dengan ukuran panjang 40 cm  (dimana tiap 1m2 = 11 buah genteng beton). Sudut kemiringan atap sebesar 35^o

 

Hitunglah luas atap dan jumlah kebutuhan atap genteng betonnya ?

1. Kita hitung dulu panjang jurai atap (warna merah), dengan rumus diatas 

Panjang jurai atap = √  ( ( 0.5 L tan α)² + 0.5 (L²)  )

                           = √  ( ( 0.5 x 6 x tan 35^o )² +  0.5 (6²)  )
                           = 4.733 m
2. Menghitung Panjang sisi miring kuda2

panjang sisi miring =   √ 2.101²  +   (1/2 L)²
                            =   √ 2.101²  +  (1/2 x 6)²
                            =     3.662 m
(Catatan : angka 2.101 didapat dari 0.5 x L x tan α)
3. Menghitung Luas Atap

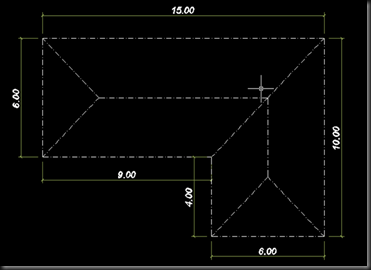
dari gambar denah atap diatas, kita bagi menjadi enam segmen luasan atap ( A, B, C, D, E, F, dan G )
biar lebih mudah, hasil perhitungan diatas kita plotkan ke gambar seperti dibawah ini.

• Luas segmen A

Luas segmen A = ( jumlah sisi sejajar x tinggi) / 2

                        = ( ( 9 + 15 ) x 3.662 ) / 2

                        = 43.944 m²

• Luas segmen B

Luas segmen B =  panjang tembereng  x  alas

                        =  4.733  x  9

                        =  42.597 m²

• Luas segmen C

Luas segmen C = (alas x tinggi) / 2 = (6 x 3.662) / 2 = 10.986 m²

• Luas segmen D

Luas segmen D = ( jumlah sisi sejajar x tinggi) / 2

                        = ( ( 4 + 10 ) x 3.662 ) / 2

                        = 25.634 m²

• Luas segmen E

Luas segmen E =  panjang tembereng  x  alas

                        =  4.733  x  4

                        =  18.932 m²

• Luas segmen F

Luas segmen F = (alas x tinggi) / 2 = (6 x 3.662) / 2 = 10.986 m²

• Total Seluruh Luasan

Luas segmen  =  A + B + C + D + E + F

                     =  43.944 + 42.597 + 10.986 + 25.634 + 18.932 + 10.986

                     =  153.079 m²

• Jumlah Atap Genteng Yang dibutuhkan

- Genteng Beton ( 1m2 = 11 buah )

- Luas Atap = 153.079 m²

- Jumlah atap genteng yang dibutuhkan = 153.079 m²  x  11 buah/m²

                                                          = 1683.689 buah

- dibulatkan menjadi = 1684 buah

Gampang kan…. Sekian dulu ulasan saya ya

semoga bermanfaat…..

Rumus Bidang Datar

Dalam perhitungan luas area sederhana secara manual, terkadang kita membutuhkan suatu rumus yang simple dan mudah diingat. Berikut adalah beberapa rumus-rumus dasar mengenai bangun bidang datar yang bisa kita gunakan untuk mempermudah perhitungan luas area. Semoga bermanfaat!

Segitiga sembarang

Rumus keliling a+b+c
Rumus Luas 1/2ct
Segitiga siku-siku

Rumus keliling a+b+c
Rumus Luas 1/2ba
Segitiga sama sisi

Rumus keliling 3a
Rumus Luas 1/2at atau 1/4 x 2a x 1,732050808

Rumus keliling a+b+c+d
Rumus Luas Luas I + Luas II
Trapesium

Rumus keliling a+b+c+d
Rumus Luas ½(b+d)t
Jajaran Genjang

Rumus keliling 2(a+b)
Rumus Luas bt
Belah Ketupat

Rumus keliling 4a
Rumus Luas at atau 1/2de
Persegi Panjang

Rumus keliling 2(a+b)
Rumus Luas ab
Bujur Sangkar (square)

Rumus keliling 4a
Rumus Luas 2a
Segienam beraturan

Rumus keliling 6a
Rumus Luas 3/2 x 2a x 1,732050808
Layang-layang (kite)

Rumus keliling a+b+c+d
Rumus Luas ef
Lingkaran (circle)

Rumus keliling 2πr^
Rumus Luas πr^2 atau 1/4 πd^2
Ellips

Rumus keliling 1/2π (a+b)
Rumus Luas π/4 x ab
Tembereng Lingkaran

Rumus keliling b + t
Rumus Luas Luas sektor – Luas segitiga

Rumus Daya dan Contoh Soal

Dalam kehidupan sehari-hari, sering kita jumpai kata watt. Misalnya setrika listrik 250 watt, lampu 20 watt. Kata watt sebenarnya adalah satuan dari daya listrik. Setrika 250 watt berarti setrika tersebut membutuhkan daya listrik 250 watt saat digunakan.
Untuk menghitung daya listrik oleh arus bolak balik (AC) dengan arus searah (DC) itu berbeda, karena arus AC mempunyai frekuensi sehingga memiliki perhitungan tersendiri. Sedangkan untuk arus DC yang melewati resistor untuk menghitung daya yang dihasilkannya dapat menggunakan rumus :
P=V.I
Dimana : P = Daya listrik dalam satuan Watt (W)
V = Tegangan listrik dalam satuan Volt (V)
I = Arus listrik dalam satuan Ampere (A)
Seperti yang kita ketahui untuk mencari Tegangan (V) dapat dihitung dengan rumus V = I.R, dimana I = Arus dan R = Hambatan, maka Rumus diatas dapat ditambahkan menjadi :
P = V. I
P = I.R.I atau P = I².R
Dari kedua rumus diatas maka dapat disimpulkan bahwa daya listrik akan bertambah besar jika :
1.       Tegangan listrik tambah besar
2.       Arus listrik tambah besar, dan
3.       Resistansi atau Hambatan tambah besar
Contoh :
Suatu senter bertegangan 30V menggunakan 2 baterai bertegangan masing-masing 1,5V. Arus yang mengalir melewati lampu sebesar 100mA. Hitung daya lampu tersebut !
Jawab :
P = V.I
P = 3x100mA
P = 300mW